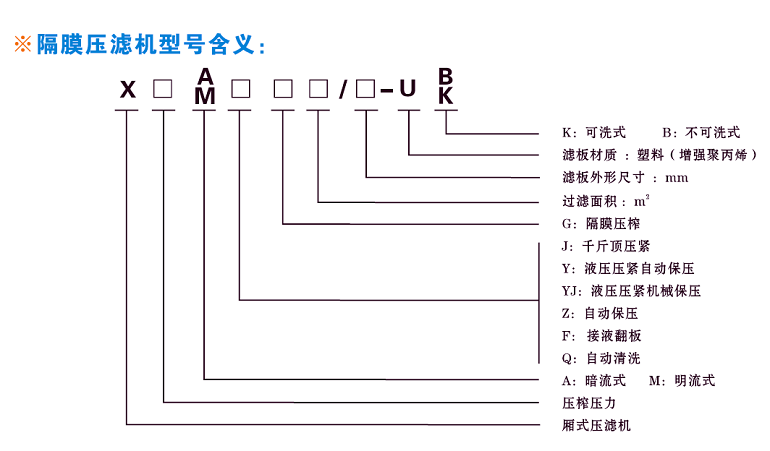
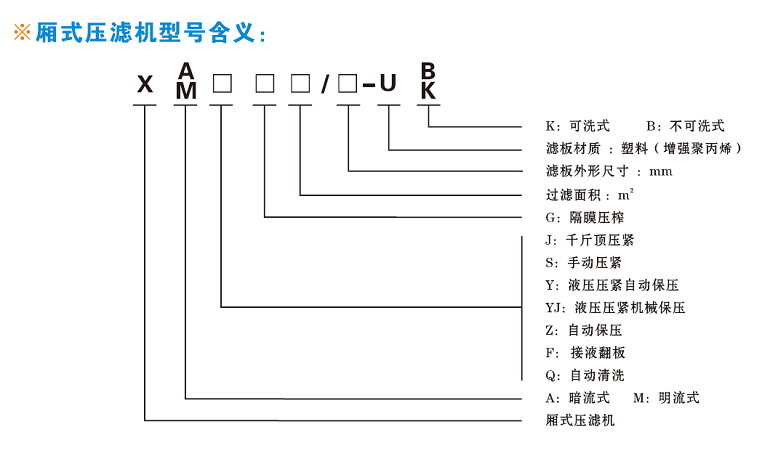
一、 压滤机设计中的数学与物理知识

压滤机的设计需兼顾过滤效率、结构强度、能耗控制三大目标，涉及流体力学、材料力学、热力学、数学建模等多领域知识。

 1.  过滤机理与流体力学基础

压滤机的核心功能是通过滤布的筛分作用实现固液分离，其过滤过程遵循“达西定律”，这是过滤系统设计的核心物理依据。

-达西定律表达式：

  Q =(K×A×ΔP)÷(μ×L)

  式中各物理量含义及单位：

  Q：过滤流量（m³/s）

  K：滤饼的渗透率（m²），与滤饼孔隙率、颗粒粒径密切相关

  A：过滤面积（m²），压滤机的核心设计参数

  ΔP：过滤介质两侧的压力差（Pa），即过滤压力

  μ：滤液的动力粘度（Pa×s），受温度、溶质浓度影响

  L：滤饼厚度（m）

-应用场景：

  设计阶段需根据达西定律计算所需过滤面积，结合物料特性（粘度、颗粒粒径）与工艺要求（处理量、过滤时间），确定滤板尺寸与数量。例如，当滤液粘度较高时，需通过增大过滤压力ΔP或过滤面积A，来保证目标过滤流量Q。

2.  滤板结构设计与材料力学计算

滤板是压滤机的核心承压部件，需承受过滤压力、压紧力的双重作用，其结构设计需满足强度与刚度要求，避免变形、破裂。

强度校核（第四强度理论）

  滤板在工作过程中承受的是复杂的平面应力状态，需采用第四强度理论（形状改变比能理论）进行强度校核，确保**当量应力不超过材料的许用应力。

第四强度理论当量应力公式：

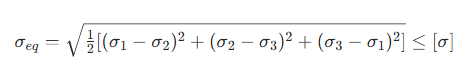
式中：σ1、σ2、σ3、 为滤板危险点的三个主应力；[σ] 为滤板材料的许用应力。

压紧力计算（静力学平衡）

  压滤机的压紧机构需提供足够的压紧力，以保证滤板之间的密封性能，防止滤液渗漏。压紧力的计算遵循静力学平衡原理：

  F压≥P滤×A封×n

  式中：

  F压：压紧机构提供的总压紧力（N）

  P滤：过滤压力（Pa）

  A封：单块滤板的密封面面积（m²）

  n：滤板数量

材料选型依据：根据强度计算结果，结合耐腐蚀性、耐磨性要求，选择聚丙烯（PP）、增强聚丙烯（RPP）、不锈钢等材料，其中高分子材料的弹性模量、泊松比等参数是刚度设计的关键。

3.  液压系统设计与流体传动原理

压滤机的压紧、拉板动作通常由液压系统驱动，其设计基于帕斯卡定律（静压传递原理）。

帕斯卡定律：在密闭容器内，施加于静止液体的压力将以等值同时传递到液体各点。

应用：液压泵输出的压力油通过管路传递到液压缸，液压缸的推力计算为：

F = P×S

  式中：F为液压缸推力（N）；P为液压系统工作压力（Pa）；S为液压缸活塞有效面积（m²）。

流量与速度的数学关系：液压缸的运动速度与输入流量成正比，公式为：

 v = Q÷S

  式中：v为活塞运动速度（m/s）；Q为液压系统流量（m³/s）。

  设计时需根据拉板、压紧的动作时间要求，计算液压系统的流量参数。

4.  过滤过程的数学建模（恒压/恒速过滤方程）

压滤机的过滤过程分为恒速过滤和恒压过滤两个阶段，通过数学建模可预测过滤时间、滤饼厚度，指导滤板结构与过滤参数设计。

恒压过滤方程：

V^{^2}+2VV_e =KA²t

式中：

V：滤液体积（m³）

V_e：虚拟滤液体积（m³），与过滤介质阻力相关

K：过滤常数（m²/s），K = 2ΔP÷μ×ρ₀（r 为滤饼比阻，ρ₀为滤饼中固相体积浓度）

t：过滤时间（s）

  该方程可用于计算达到目标滤液体积所需的时间，或根据过滤时间反推所需过滤面积。

二、 压滤机选型中的数学与物理知识

压滤机选型的核心是匹配物料特性与工艺要求**，需通过定量计算确定过滤面积、过滤压力、滤板材质等关键参数，避免“大马拉小车”或“小马拉大车”的资源浪费。

1.  过滤面积的精准计算（核心选型参数）

过滤面积是决定压滤机处理能力的关键，其计算基于物料处理量和过滤速度，结合达西定律与生产工况推导。

选型计算公式：

  A = (Q×μ×L)÷(K×ΔP)

  实际应用中，需结合现场物料的小型过滤试验数据（如实验室滤压试验测得的渗透率$K$、滤饼厚度L），代入公式计算理论过滤面积，再乘以1.1～1.3的安全系数，确定最终选型面积。

物理依据：物料的颗粒粒径越小、粘度越高，滤饼渗透率K越小，所需过滤面积越大；提高过滤压力ΔP可减小所需面积，但需考虑滤板的耐压极限。

2.  过滤压力的选型依据（流体力学与物料特性结合）

过滤压力的选择需兼顾分离效率与设备成本，其核心物理逻辑是：压力越高，滤饼孔隙率越低，滤液含固量越低，但设备的密封要求、结构强度要求也越高。

选型原则：通过物料压缩性试验确定临界过滤压力——当压力升高到某一值后，滤饼比阻r不再显著降低，此时的压力即为**过滤压力。

数学验证：根据滤饼比阻公式 r = r₀×ΔP^s（r₀为初始比阻，s为压缩指数），当 s=0 时，滤饼为不可压缩性，可适当提高压力；当 s>0 时，滤饼为可压缩性，过高压力会导致滤布堵塞，降低过滤效率。

3.滤布选型的物理原理（筛分效应与表面张力）

滤布是过滤介质，其选型基于颗粒筛分和表面润湿的物理原理：

筛分效应：滤布的孔径需小于物料中固相颗粒的粒径，且大于滤液分子尺寸，遵循“筛分截留”原理。实际选型中，滤布孔径通常为颗粒粒径的0.5~0.8倍，防止颗粒穿滤。

表面张力与润湿性：根据滤液的极性选择滤布材质——亲水性滤布（如涤纶、丙纶）适用于水性滤液，疏水性滤布（如聚四氟乙烯）适用于油性滤液，利用表面张力差异提高过滤效率。

4.处理量的校核计算（物料衡算）

选型后需通过物料衡算验证设备处理量是否满足工艺要求，遵循质量守恒定律：

固相物料衡算：

Q_{_m} = （V×ρ_s×ω）÷t

  式中：

  Q_{_m}：固相处理量（kg/h）

  V：单批次滤液体积（m³）

  ρ_s：固相密度（kg/m³）

  ω：料浆固相质量分数

  t：单批次过滤时间（h）

若计算出的Q_{_m}小于工艺要求，需增大过滤面积或提高过滤压力。

三、 压滤机应用中的数学与物理知识

压滤机在实际运行中的工况优化、故障诊断、能耗控制，均需通过数理知识进行定量分析，实现高效运行。

1.工况参数优化（基于过滤方程的动态调整）

实际运行中，可通过监测滤液流量、过滤时间等参数，代入恒压过滤方程，优化操作参数：

当过滤时间延长、流量下降时，表明滤饼比阻r增大，可通过提高洗涤水压力（降低滤饼比阻）或缩短过滤周期（减少滤饼厚度）来改善；

当滤液含固量超标时，可根据筛分原理，更换孔径更小的滤布，或适当降低过滤速度，提高截留效果。

2.洗涤过程的物理与数学分析

滤饼洗涤是压滤机应用的重要环节，目的是置换滤饼中残留的滤液，其效果基于对流扩散原理。

洗涤效率计算：

式中：Cw为洗涤后滤饼中溶质浓度；C₀为洗涤前溶质浓度。

物理优化方法：采用逆流洗涤（洗涤液与滤液流向相反），利用浓度梯度提高扩散效率；控制洗涤液温度，通过降低滤液粘度（物理性质），提高洗涤速度。

3.能耗计算与节能优化（热力学与流体力学结合）

压滤机的能耗主要来自液压系统和进料泵，通过数理计算可实现节能优化：

进料泵能耗计算：

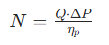
式中：N为进料泵功率（kW）；ηp为泵的效率。

节能原理：通过优化进料压力，避免“超压进料”当压力超过滤饼临界压缩压力后，能耗增加但过滤效率提升有限，此时可适当降低压力，实现能耗与效率的平衡。

4.  故障诊断的数理分析

压滤机运行中的常见故障（如滤液渗漏、滤板变形），可通过数理知识定位原因：

滤液渗漏：若单块滤板渗漏，可能是压紧力不足，可通过压紧力公式 F_压＞F_滤＞A_封 ×n校核，增大液压系统压力；若多块滤板渗漏，可能是滤板密封面磨损，需测量密封面平整度（几何量），更换或修复滤板。

滤板变形：通过测量滤板的形变量（如挠度），结合材料力学的挠度公式w=5qL⁴（q为均布载荷，E为弹性模量，I为截面惯性矩），判断是否因过滤压力超标或材料强度不足导致，进而调整工况或更换滤板。

四、总结

数学与物理知识是压滤机设计的理论基础、选型的定量依据、应用的优化工具。从达西定律指导过滤面积设计，到材料力学支撑滤板结构强度，再到物料衡算验证设备处理能力，数理知识贯穿于压滤机全生命周期。对于行业从业者而言，掌握这些数理知识，能够实现设备的精准研发、科学选型与高效运行，从而提升固液分离工艺的经济性与可靠性。

另外还有以下知识：

压滤机的过滤和分离，用到的数学知识和物理化学的知识，主要是过滤量，原浆含固率、滤饼容量、进料压力，和压紧压强、液压系统压力、电器系统功率等方面的计算；试列举如下：
1，压滤机滤室容量计算
1) 参数设定:
原浆(处理前的悬浮液)体积为：V1(M3)
原浆含固率(干灰)：δ1(%)
滤饼含固率：δ2(%)
滤饼的体积：V2(m3)
过滤浓缩比：Δ=δ1(%)÷δ2(%)
压滤机单位容积：v( 15L/ m2)
压滤机的过滤速度：s（L/h×m2）
压滤机过滤面积：M(m2)
压滤机的过滤周期：T
2）公式计算：
∵ V2(m3) ×δ2(%)= V1(m3) ×δ1(%)
∴ V2(m3)= V1(M3) ×δ1(%)÷δ2(%)=V1(M3) ×Δ
即：滤饼的体积=原浆的体积×浓缩比
∵ 滤饼的体积V2(M3) ÷压滤机单位容积v( 0.015 M3/ m2)=过滤面积M(m2)
∴ 过滤周期T=滤饼的体积V2(M3) ÷压滤机的过滤速度s（M3/h×m2）÷过滤面积M(m2)
即：过滤周期=滤饼体积×过滤面积÷过滤速度
2，压滤机压紧力计算
A．压滤机额定进料压力F1= P1×S1
        P1：液压系统压强；S1：液压缸缸内径面积
B．滤室部分反推压力F2= P2×S2
1）滤室内工作压力受制于压滤机的压紧压力，即压滤机机架等所允许的**操作压力。
2）滤板在一定的操作温度下所允许的**操作压力。
3）F1>F2(压紧压力应大于进料压力)。
P2：工作压强（过滤、洗涤、吹风、压榨）；S2：滤室内的有效作用面积
举例：XY1250型压滤机，液压压紧自动保压。进料压力≤1.0MPa；配25MCY14-IB柱塞泵，泵压力≤31.5Mpa；油缸内径Φ280。求：**压紧力F1和**反推力F2
解：F1≤P1×S1=31.5MPa×0.14m2×π=31.5kgf/cm2×6.1544c m2=193.86 kgf≈1939KN ；（1N=9.8kg≈10kg）即：F1≤1939KN
F2≤ P2×S2=1.0MPa×1150mm×1150mm=1.0 kgf/cm2×132.25 cm2=132.25 kgf≈1323KN  即： F2≤1323KN；那么 F1＞F2
3，压滤机设计理论计算用到的物理公式如下：
1）机械应力
Pa=1N/㎡  Mpa=106Pa  1Mpa=9.8kgf/cm2≈10.0kgf/cm2 ；
压紧力F=1.0kgf=9.8N≈10N  1KN≈100 kgf=0.1t
物理学公式：重量(G)= m(质量kg) ×g(9.8重力加速度kg/N)=9.8N
1N=1/9.8kg≈0.10204kg≈1/10kg=0.1kg
2）压力转换
标准大气压：atm=101325pa 工程大气压：at=98066.5pa

泵的扬程和压力成正比和对等的！1bar=10米=0.1Mpa；1毫米汞柱 = 133.322368 帕斯卡

3) 质量转换
1g水=1mL×1(水的密度ρ=1)=1 cm3×1(水的密度ρ=1)
1kg水=103mL×1(水的密度ρ=1) ==1L×1(水的密度ρ=1)=1dm3×1(水的密度ρ=1)
1t水=1000L×1(水的密度ρ=1) =1000dm3×1(水的密度ρ=1)=1 m3×1,(因为水的密度ρ=1)
物理学公式：质量(m)= ρ(密度/比重) ×v(体/容积)
重量(G)= m(质量kg)×g(9.8重力加速度kg/N)=ρ(密度/比重)×v(体/容积)×g(9.8重力加速度kg/N)；
如您在压滤机、过滤工程选型中需要理论数据的，欢迎来电咨询，我们可根据您现场过滤工况和您共同做好设备方案设计和科学选型。

如您在压滤机、过滤工程选型中需要更多的过滤与分离方面的咨询，欢迎来电（13732231928周经理）咨询，我们可根据您现场过滤工况和您共同做好设备方案设计和科学选型。